Overview

An essential first step before conducting statistical analysis of data – even before deciding which statistical analysis to conduct – is understanding the distribution of those data.

Many statistical models have one or more assumptions about the nature of the data being tested, and several assumptions refer to the distribution. Importantly, not all models have the same assumptions, or even apply to the same types of data. Thus it is critical to first understand the type of data, and then the distribution of those data, before selecting a statistical model to ensure that an appropriate test is performed.

As this lesson will show, using data distributions to select an appropriate model is not just pedantic nerdiness. Often, fitting a specific model will lead to better outcomes than sticking to standard statistical tests.

This lesson shows how to find data moments and plot distributions with ggplot. The nuts and bolts of distributions and model assumptions are beyond the scope of this Intro course, but I’ve written about it elsewhere.

Objectives

Use ggplot to present data distributions using
- geom_histogram
- geom_density
- stat_function
Use MASS::fitdistr() to estimate distribution parameters
Apply distribution functions d*dist and r*dist for normal, log-normal, and gamma distributions
Use quantile() to calculate confidence intervals from simulated datasets

Materials

Script

IntroDistributions.R

Walking through the script

Load packages. permute has an example dataset we’ll play with in this lesson, after first converting to a tibble object:

pacman::p_load(tidyverse, permute)
data(jackal)
(jackal <- as_tibble(jackal))

## # A tibble: 20 x 2
##    Length Sex   
##     <dbl> <fct> 
##  1    120 Male  
##  2    107 Male  
##  3    110 Male  
##  4    116 Male  
##  5    114 Male  
##  6    111 Male  
##  7    113 Male  
##  8    117 Male  
##  9    114 Male  
## 10    112 Male  
## 11    110 Female
## 12    111 Female
## 13    107 Female
## 14    108 Female
## 15    110 Female
## 16    105 Female
## 17    107 Female
## 18    106 Female
## 19    111 Female
## 20    111 Female

Some basics of statistics

To understand why data distributions are so important to picking a good statistical model, let’s review some of the basic reasons for using statistics in the first place.

A potential research question for these data might include: Does the length of jackal teeth vary by sex?

The typical approach would be to measure the length of male and female jackal teeth and compare the average length of teeth by sex:

jackal %>% 
  group_by(Sex) %>%
    summarise(Mean=mean(Length) ) %>%
  knitr::kable()

Sex	Mean
Male	113.4
Female	108.6

We can see that the average male jackal has longer teeth than the average female jackal. But this does not necessarily mean that any random male jackal is likely to have longer teeth than any random female jackal, which is more convincing evidence in terms of the initial research question.

To determine how well the average jackal of a particular sex represents any random jackal of that sex, we need to look at the variability of the data around that mean. The closer most jackals of a particular sex are to the mean, the more robust of an estimate the mean represents. But if the individual observations are scattered widely around the mean value, the mean is mostly just an arithmetic value that has little use to us in describing biological patterns.

Variability around the mean can be assessed by standard deviation, which is typically a measure of variability in the broader population (e.g., all the jackals), or the standard error, which can be interpreted as how precisely the mean of a sample represents the mean of the population (e.g., these 10 jackals vs all the jackals out there); if variability in the population is high, it is unlikely that the sample mean overlaps well with the population mean.

jackal %>% 
  group_by(Sex) %>%
    summarise( 
       Mean = mean(Length), 
       SD = sd(Length), 
       SE = sd(Length)/sqrt(length(Length))) %>%
  mutate_at(vars(SD, SE), ~round(., 2)) %>%
  knitr::kable()

Sex	Mean	SD	SE
Male	113.4	3.72	1.18
Female	108.6	2.27	0.72

Just looking at these tables, though, doesn’t give us much of an idea of how much variability is actually around the mean.

Let’s plot the data:

jackal %>% 
  group_by(Sex) %>%
    summarise( 
       Mean = mean(Length), 
       SE = sd(Length)/sqrt(length(Length))) %>%
  ggplot(aes(x=Sex)) + theme_bw(16) +
    geom_jitter(data=jackal, 
                aes(y = Length), 
                width = 0.15, 
                alpha = 0.5) + 
    geom_errorbar(aes(ymin = Mean - SE, 
                      ymax = Mean + SE), 
                  width = 0.1, 
                  size = 1) +
    geom_point(aes(y = Mean), 
               pch = 17, 
               size = 5)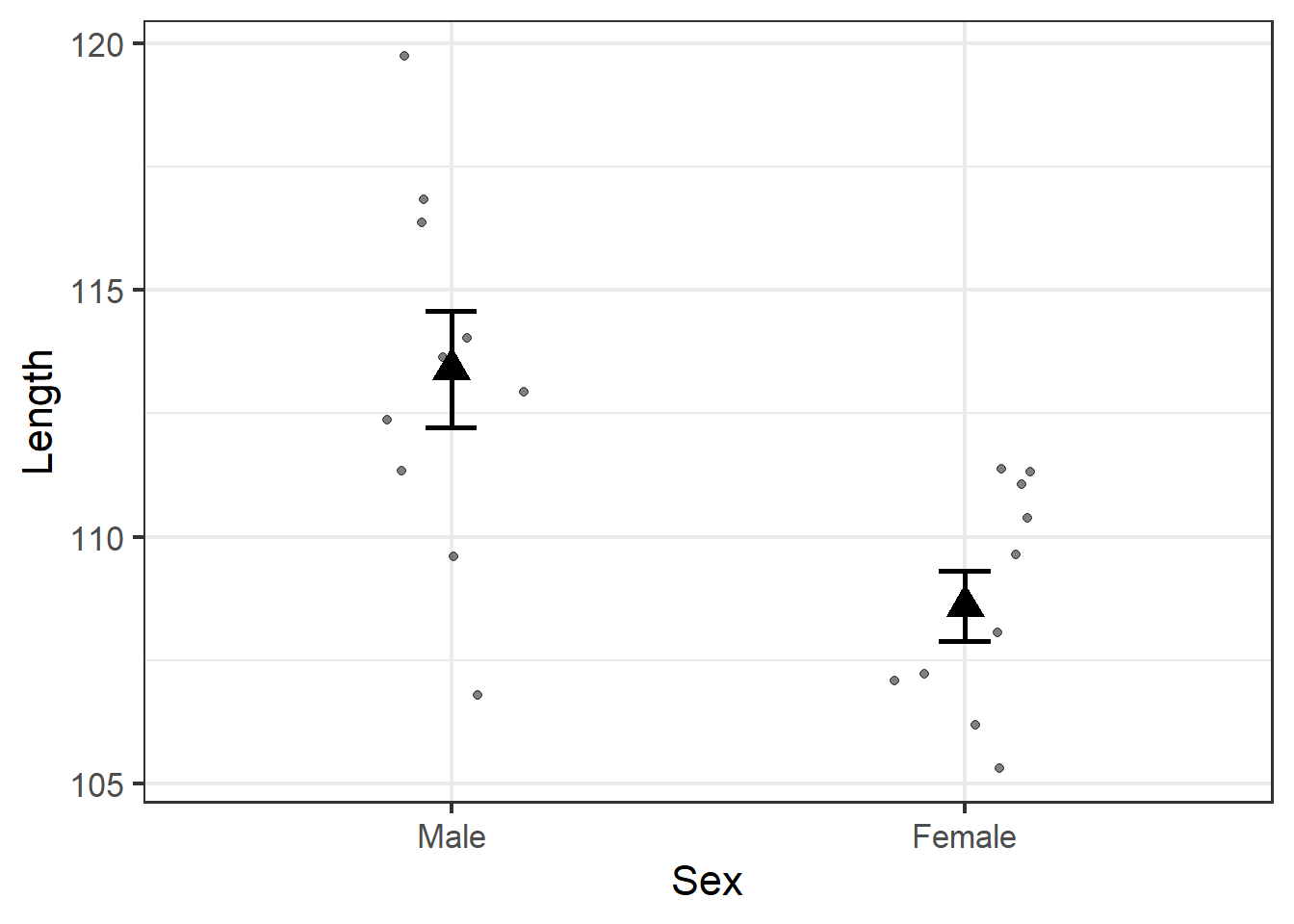

We already knew the average male jackal had longer teeth than the average female, but this plot illustrates the degree to which observations for each sex overlap. Indeed, several females have longer teeth than several males, and one male even has shorter teeth than the average female.

But the error bars do not overlap, which gives us our first indication that the fact that the average male tooth length is longer than the average female tooth length is a legitimate biological trend in this jackal population.

The next step would be to test this statistically – what is the probability that the pattern in the sample data is due to chance regarding our sampled jackals, rather than a real biological pattern among jackals?¹

For a statistical model to give us insight into a population based on a sample, it makes some assumptions about patterns in the population that we probably don’t know, and must infer from our sample data. Thus, if our data don’t match those assumptions, we cannot reliably extend the model’s analysis of our data to the broader population.

If you’ve heard about assumptions before, you’re probably most familiar with the assumption of normality, which means the data are distributed in a bell-shaped curve: most observations are close to the mean, with very few low and high values:

Figure 1: A typical normal (aka Gaussian) distribution with mean = 0 and sd = 3.

Nearly 15% of observations have a value of 0, while values of -5 and below, and 5 and above, comprise less than 5% of observations together (2.5% each).

The general bell curve is the theoretical shape of any normally-distributed population. The specific shape – steepness of slope, sharpness of point – are determined by the variance (here, sd = 3), while the values along the bottom depend on the actual range of the data.

Plotting distributions

Let’s see how our sample data on jackal look in terms of the expected bell curve shape.

There are three components to plotting distributions in ggplot. Each step connects the data in the sample to the theoretical distribution the model assumes the population must have.

Histogram

We use geom_histogram to plot our actual data from the sample. It is a bit different than other geoms:

When y = ..density.. it knows we want to see the data’s distribution, and we only assign one aesthetic from variables in our dataset as x=, which is the specific vector in the dataset we want to see the distribution of.
binwidth= is an important argument that can take trial and error to get right. Set binwidth too small, and there will be odd gaps between the bars, or it will take a long time to render the plot. Set binwidth too high, and you won’t see patterns in the data.

jn_gg <- ggplot(jackal, aes(x=Length)) + theme_bw(16) + 
              geom_histogram(aes(y=..density..),      
                 binwidth=1,
                 colour="black",
                 fill="lightgreen") 
jn_gg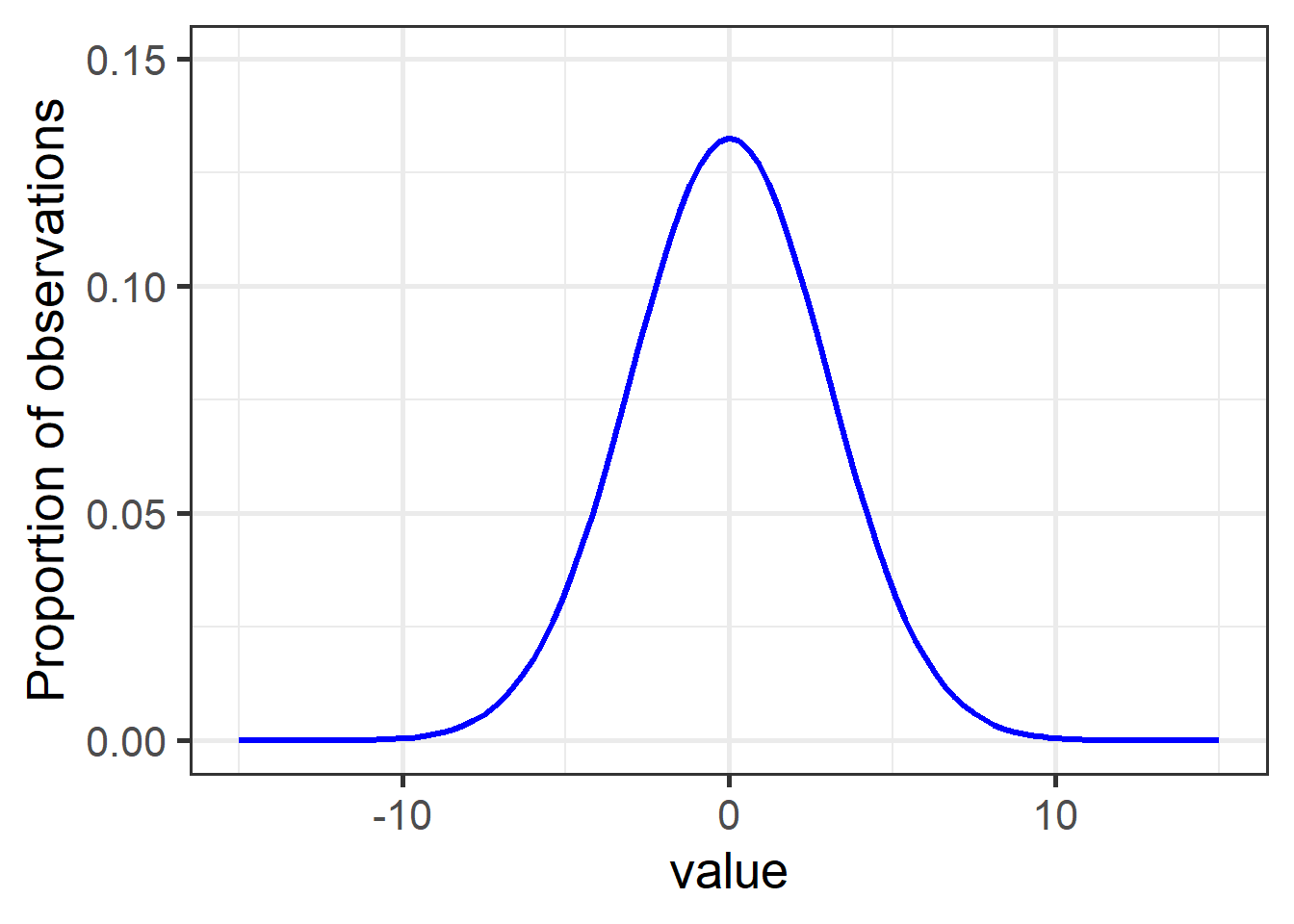

Kernel density estimate

The second step starts to connect patterns in our sample data to what the population might look like. geom_density smooths the trend of the binned histogram bars using what’s called a kernel density estimate. If there are gaps in our sample data, the density estimates what the missing values might be, giving a better approximation of the potential distribution of the data had we collected more samples:

jn_gg <- jn_gg + geom_density(alpha=.5, fill="lightblue")
jn_gg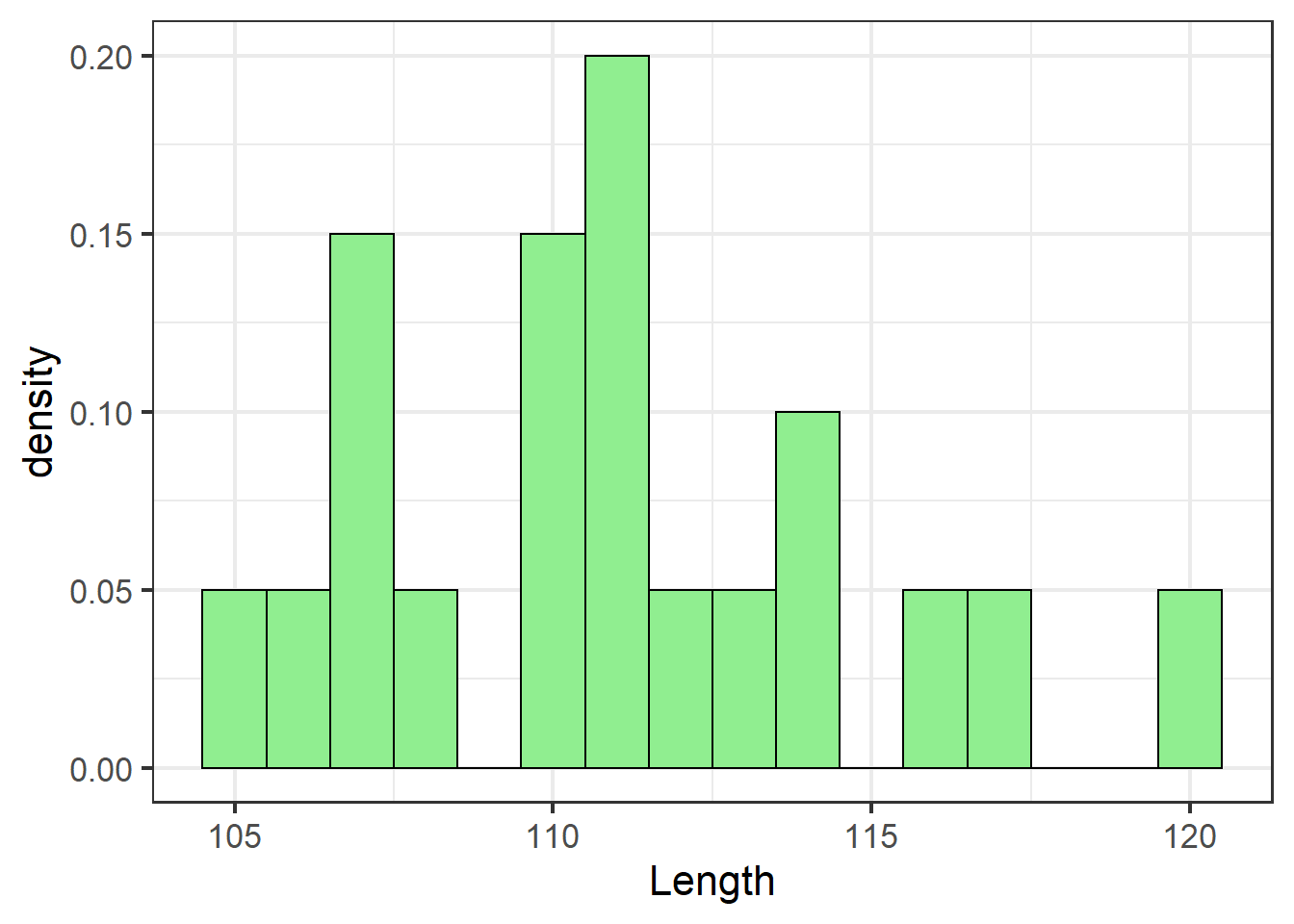

Even though our sample doesn’t include an observation with tooth length 115, the density estimate suggests about 5% of jackals would have tooth length 115 if we had a more complete sample.

Moments

The third step is to take what we know about the distribution of our sample data and estimate the distribution of the population. This is the assumption that the statistical model will make: the population distribution can be described by moments of the data:

The first moment is the mean
The second moment is the variance

All theoretical distributions can be described in terms of these two moments: the mean \(\mu\) and the variance \(\sigma^2\). But as we can infer from the density plot, there can be some error in the moments of our sample data and what we’d find if we had a better, or even different, sample.

We can use the fitdistr function from the default MASS library to estimate robust parameters for distributions based on our sample data.² Just give it the vector and the desired distribution:

MASS::fitdistr(jackal$Length, "normal")

##       mean           sd     
##   111.0000000     3.7815341 
##  (  0.8455767) (  0.5979130)

The normal distribution uses the raw moments as parameters.³ This represents the theoretical distribution of the population assumed by a test based on the normal distribution.⁴

We add the theoretical distribution using a new element of ggplot: instead of a geom, we use a stat, specifically stat_function, which chugs a function (defined as fun =) in the background and adds the results to the plot.

\({\bf\textsf{R}}\) has many functions for distributions. All have two parts:

The first part is either d, r, p, or q. Right now, we only care about d*dist and r*dist.
- d refers to density, and returns the theoretical distribution curve.
- r stands for random, as in random number, and returns a defined number of random draws from a given distribution.
The second part (*dist) defines which distribution to use. In this case, we want norm, for the normal distribution.

Putting this together, we assign fun = dnorm for stat_function to give us the theoretical normal distribution.

One last step: Assign the parameters. Each *dist or *dist function needs to know the parameters of the data. dnorm needs \(\mu\) and \(\sigma^2\). Since stat_function is running dnorm in the background and plotting the results, we need stat_function to pass the parameters on to dnorm for us. This is accomplished with args=. We give args= a list of arguments that dnorm needs.

stat_function technically doesn’t use these arguments itself, so looking up ?stat_function won’t help figure out what arguments to pass. ?dnorm will.

Remember, we got our parameter estimates from MASS::fitdistr():

jn_gg <- jn_gg + 
          stat_function(data=jackal, 
                       fun = dnorm, 
                       args=list(mean = 111,
                                 sd = 3.78),
                       colour="blue", 
                       size=1.1) 
jn_gg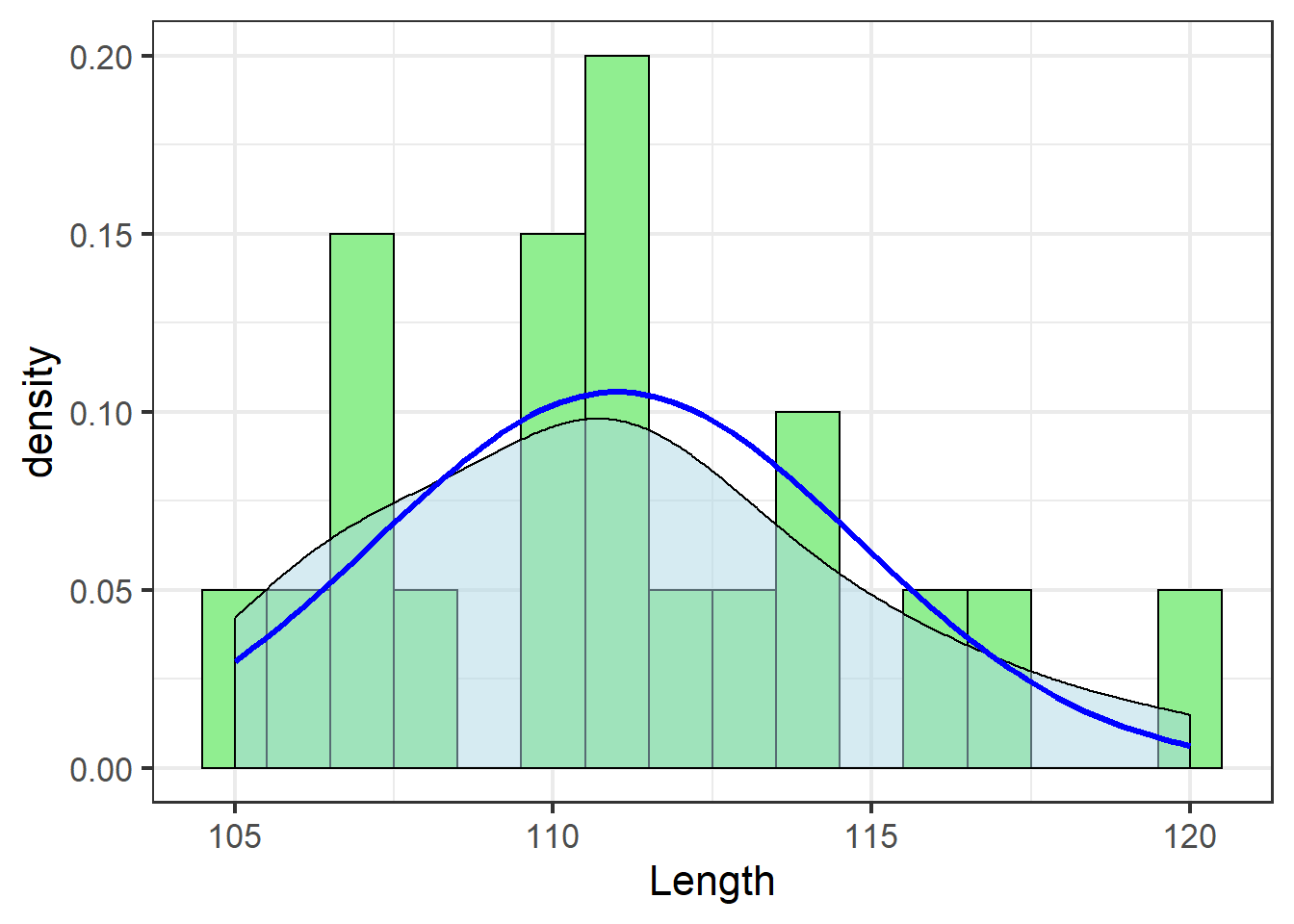

The blue line shows the theoretical distribution of the data – the distribution of the population assumed by a statistical model based on the normal distribution.

If the distribution of the sample data do not match this theoretical distribution well, it is inappropriate to use a statistical test that assumes a normal distribution, and results of such a test, even if it runs without an error, are not to be trusted.

Let’s zoom out a bit to get a better idea of the assumed distribution:

jn_gg <- jn_gg + xlim(c(mean(jackal$Length)-15, 
                      mean(jackal$Length)+15))
jn_gg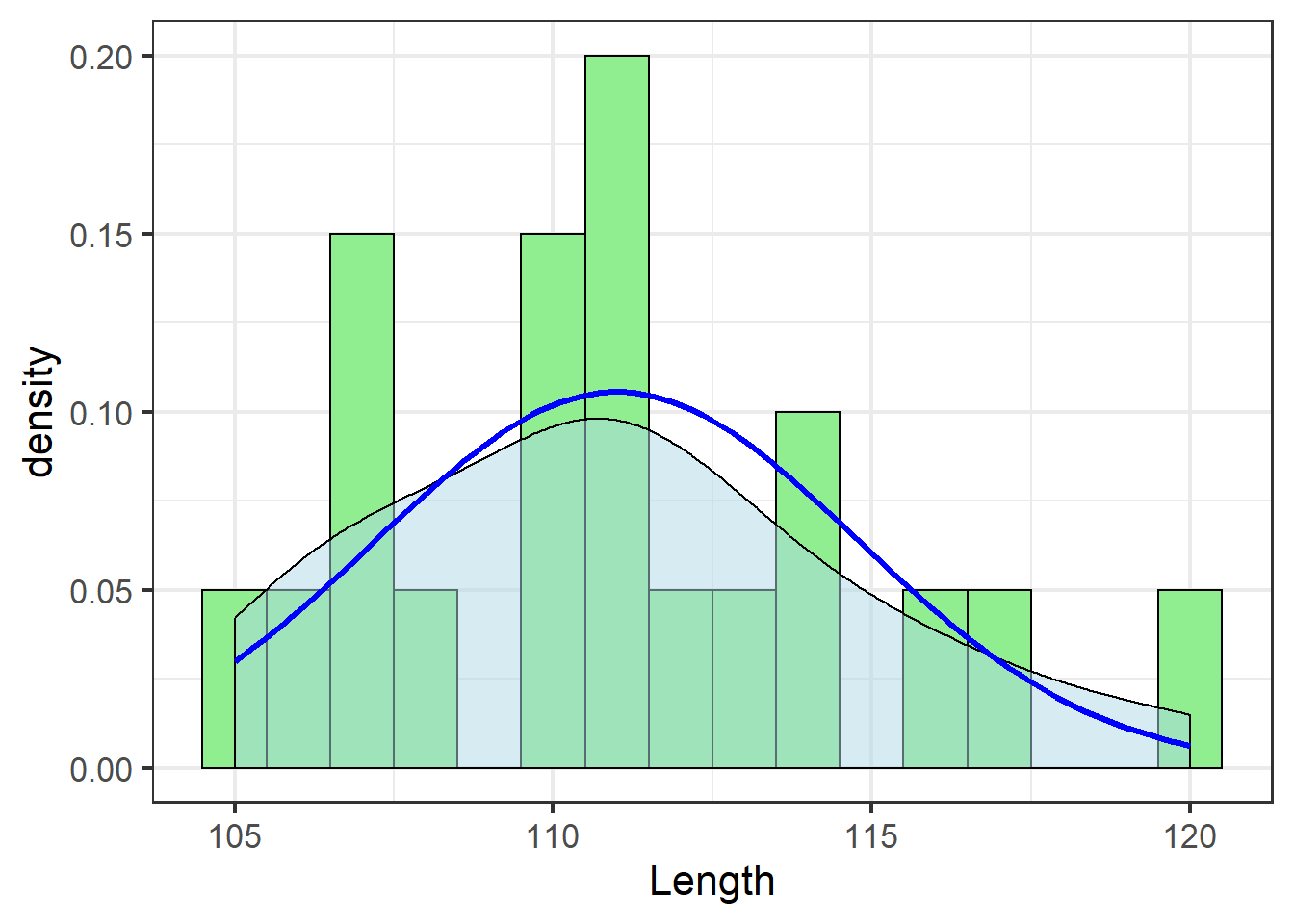

Assessing fit

While it can be difficult to compare the histogram (green bars) and the theoretical distribution (blue line), the density estimate (shaded area) helps.

In this case, the blue line and the shaded area match pretty well. This is a subjective assessment based on one’s own visual analysis of the plot. While there are statistical tests out there one can use to determine whether the data fit the assumed distribution “well enough,” I discourage their use because there are concerns about sensitivity to sample size. Yes, distributions are important. No, we don’t need to get really anal about testing them – visual assessment is fine.

One major source of poor fit is skewness, which refers to an asymetrical distribution visualized as a tail on one side or another of the bell curve.

A quick way to quantify skewness is to calculate the ratio between the mean and the median. Data that follow a perfectly normal distribution will have identical mean and median, with exactly half of the data on each side of the mean:

knitr::kable(
  tibble(Mean = mean(jackal$Length), 
         Median = median(jackal$Length), 
         Ratio = Mean/Median)
  )

Mean	Median	Ratio
111	111	1

Deviations beyond 0.95 – 1.05 are worth looking into.

Improving fit

Clearly these data don’t need much work, but we’ll use them to demonstrate some options to correct for skewness.

In general, if data do not match a given distribution, one has two options:⁵

Transform the data such that they better fit the distribution
Fit a different distribution

Transformations

A transformation is a mathematical operation applied to each data point that alters their value and thus changes the shape of the distribution. Importantly, a transformation does not change the relative values of the observations, so a point with a lower value than another in the raw data set will still have a lower value in the transformed data set. However, their values will be changed and they will likely have more or less space between them on the new scale.

In the context of the normal distribution, the log transformation is likely the most frequently-encountered solution to skewness. In the log transformation, each value is essentially reduced by an order of magnitude, so points that occur out on the tail of a skewed distribution are brought closer to the median. As such, the effectiveness of the log transformation is greatest when the original data scale spans at least one order of magnitude, but not so many that dropping one order of magnitude doesn’t have much of an effect.

To view the distribution of log-transformed data in \({\bf\textsf{R}}\), one can either apply the transformation to the data themselves with the log() function…

mutate(jackal, LogLength = log(Length))

## # A tibble: 20 x 3
##    Length Sex    LogLength
##     <dbl> <fct>      <dbl>
##  1    120 Male        4.79
##  2    107 Male        4.67
##  3    110 Male        4.70
##  4    116 Male        4.75
##  5    114 Male        4.74
##  6    111 Male        4.71
##  7    113 Male        4.73
##  8    117 Male        4.76
##  9    114 Male        4.74
## 10    112 Male        4.72
## 11    110 Female      4.70
## 12    111 Female      4.71
## 13    107 Female      4.67
## 14    108 Female      4.68
## 15    110 Female      4.70
## 16    105 Female      4.65
## 17    107 Female      4.67
## 18    106 Female      4.66
## 19    111 Female      4.71
## 20    111 Female      4.71

… or simply use the log-normal distribution:

MASS::fitdistr(jackal$Length, "lognormal")

##      meanlog        sdlog   
##   4.708955927   0.033804989 
##  (0.007559025) (0.005345038)

jn_gg + 
  stat_function(data=jackal, 
                fun = dlnorm, 
                args=list(meanlog=4.71,
                          sdlog=0.03),
                lty=5,
                colour="blue", 
                size=1.1)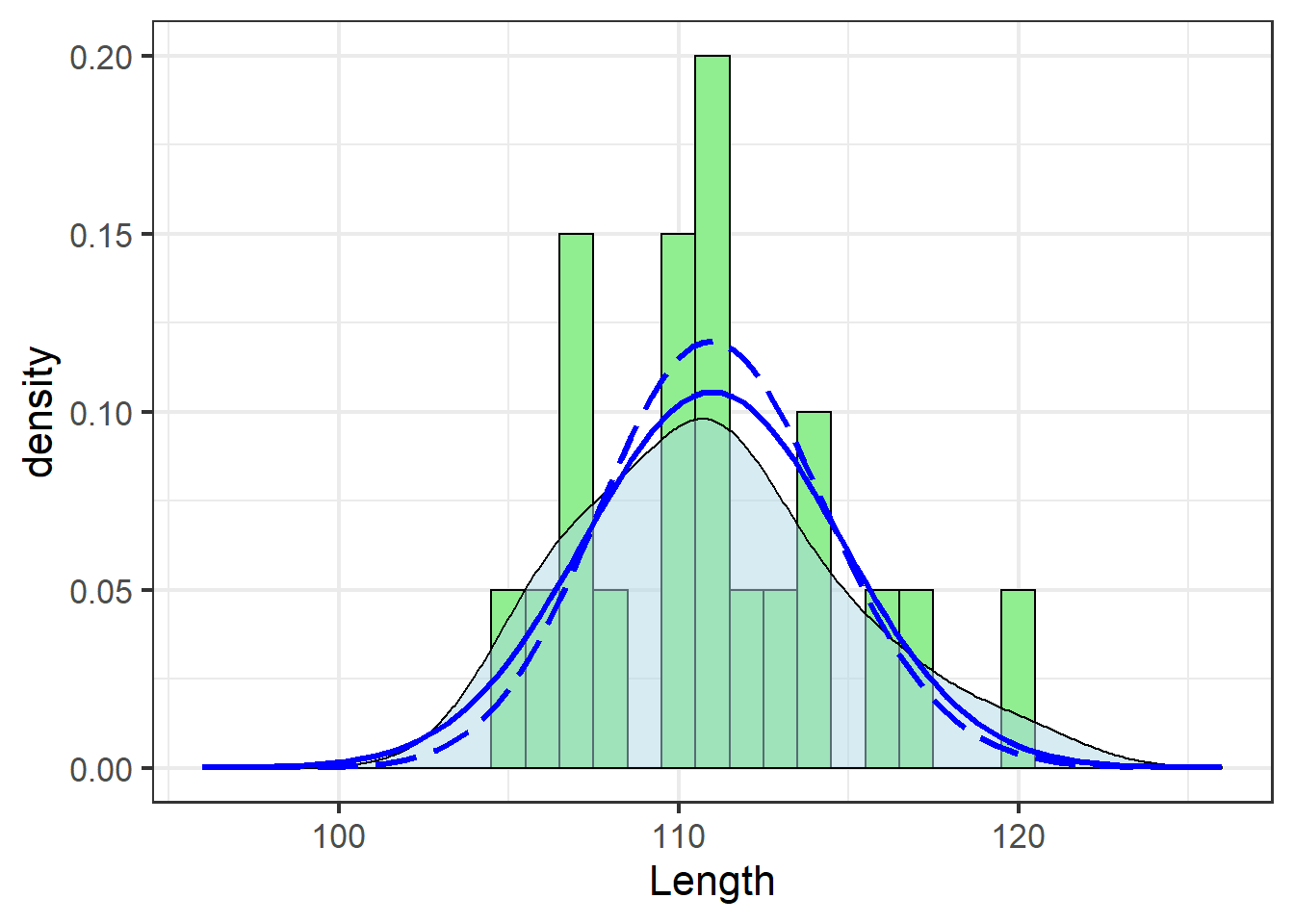

Note the use of dlnorm in place of dnorm to fit the log-normal distribution, and the different parameters passed via args=. dnorm could just as easily be used if the underlying data were first log-transformed, which would require redrawing the plot or some other tricks.

These data didn’t need the transformation (and the solid blue line actually traces the density estimate best), but the effect is apparent: a tighter fit around the mean.

Alternative distributions

When transformations are either not desired or not effective in getting data to fit a normal distribution, an alterative is to use a statistical model that assumes the data fit a different distribution. Generalized linear models are examples of regression models in which the distribution is specified. One determines the most appropriate distribution via the same steps as above, using MASS::fitdistr() and d*dist and r*dist distribution functions.

The gamma distribution is often a good alternative for skewed data.⁶ The following example demonstrates the utility of the gamma distribution over the normal distribution, even though the latter would technically work with these data.

These data come from a paper on raptor responses to prescribed fire. We can load them directly from the course GitHub site:

load(url("https://github.com/devanmcg/IntroRangeR/raw/master/data/swha.dat.Rdata") )
as_tibble(swha.dat)

## # A tibble: 18 x 7
##     burn  year species pre.count dur.count   sum  diff
##    <int> <int> <fct>       <dbl>     <dbl> <dbl> <dbl>
##  1     6  2014 SWHA            0        18    18    18
##  2     7  2014 SWHA            0        11    11    11
##  3     8  2014 SWHA            0        19    19    19
##  4     9  2014 SWHA            0         8     8     8
##  5    10  2014 SWHA            0        43    43    43
##  6    11  2014 SWHA            1        16    17    15
##  7    14  2015 SWHA            0         6     6     6
##  8    15  2015 SWHA            0        15    15    15
##  9    16  2015 SWHA            0         7     7     7
## 10    17  2015 SWHA            0         9     9     9
## 11    18  2015 SWHA            0        44    44    44
## 12    19  2015 SWHA            0        39    39    39
## 13    20  2015 SWHA            0        16    16    16
## 14    21  2015 SWHA            4        51    55    47
## 15    22  2015 SWHA            0        10    10    10
## 16    23  2015 SWHA            0         7     7     7
## 17    24  2015 SWHA            4        12    16     8
## 18    25  2015 SWHA            3         3     6     0

The hypothesis was that raptors were attracted to fires, so observers counted the number of raptors before and during burns. The only species that demonstrated an effect was Swainson’s Hawk, so the data are trimmed to SWHA. The analysis focused on the change in counts, during - before, represented by the variable diff:

swha_gg <- ggplot(swha.dat, aes(x=diff)) + theme_bw(16) + 
            geom_histogram(aes(y=..density..),      
                           binwidth=1,
                           colour="black", 
                           fill="lightgreen") +
            geom_density(alpha=.2, fill="#FF6666")  
swha_gg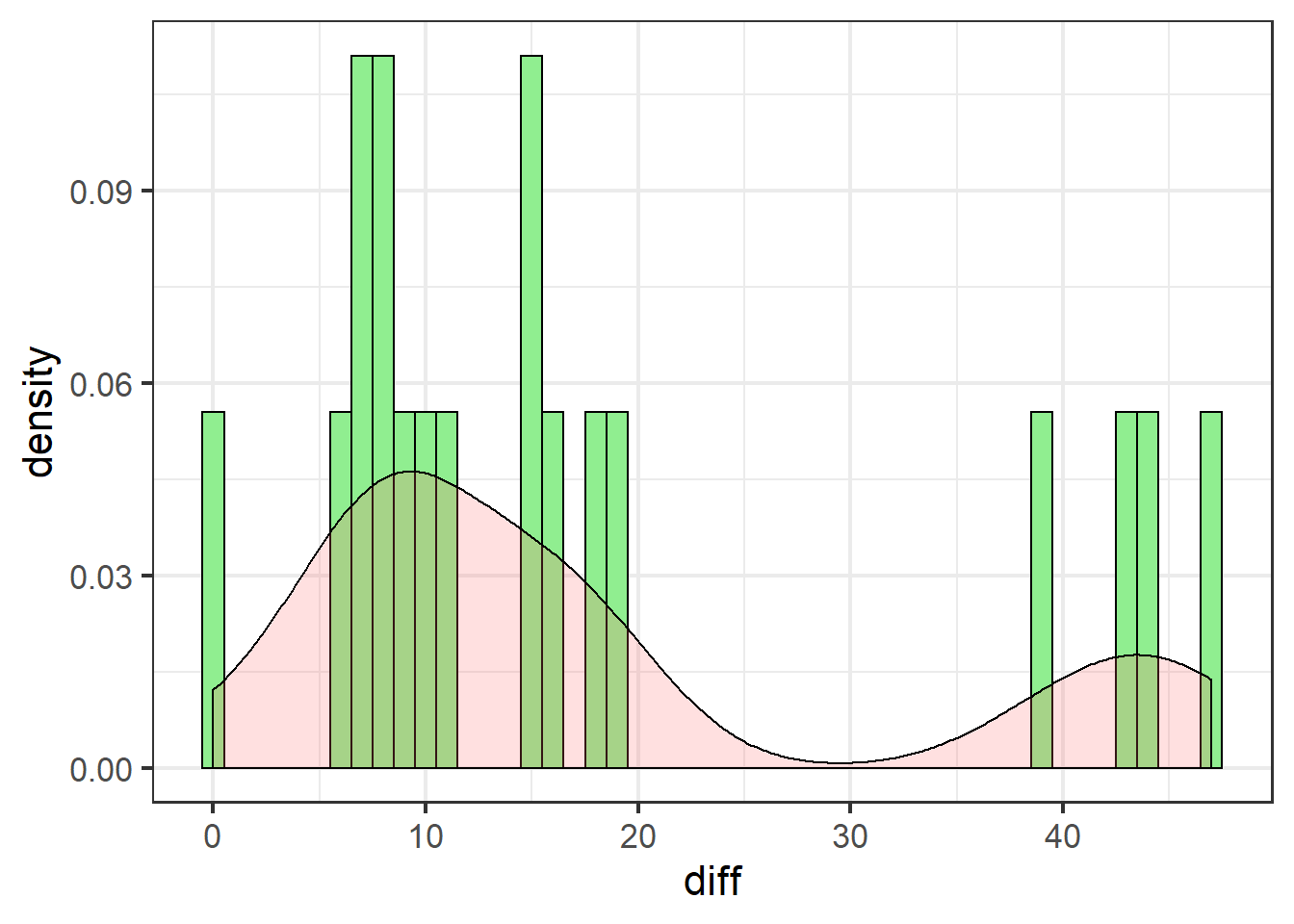

These data are definitely not normally distributed. There are several cases of very high differences. All data are either positive, or zero (no effect).

Let’s add the theoretical normal distribution, and see if the log-normal does any better:

swha_gg + 
  stat_function(data=swha.dat, 
                fun = dnorm, 
                args=list(mean=mean(swha.dat$diff),
                          sd=sd(swha.dat$diff)),
                colour="blue", 
                size=1.1)  + 
  xlim(c(-30, 60))  + 
  stat_function(data=swha.dat, 
                fun = dlnorm, 
                args=list(meanlog=mean(log(swha.dat$diff+1)),
                          sdlog=sd(log(swha.dat$diff+1))),
                colour="blue", 
                lty=5,
                size=1.1)  + 
  labs(title = "Normal (Gaussian) & log-normal")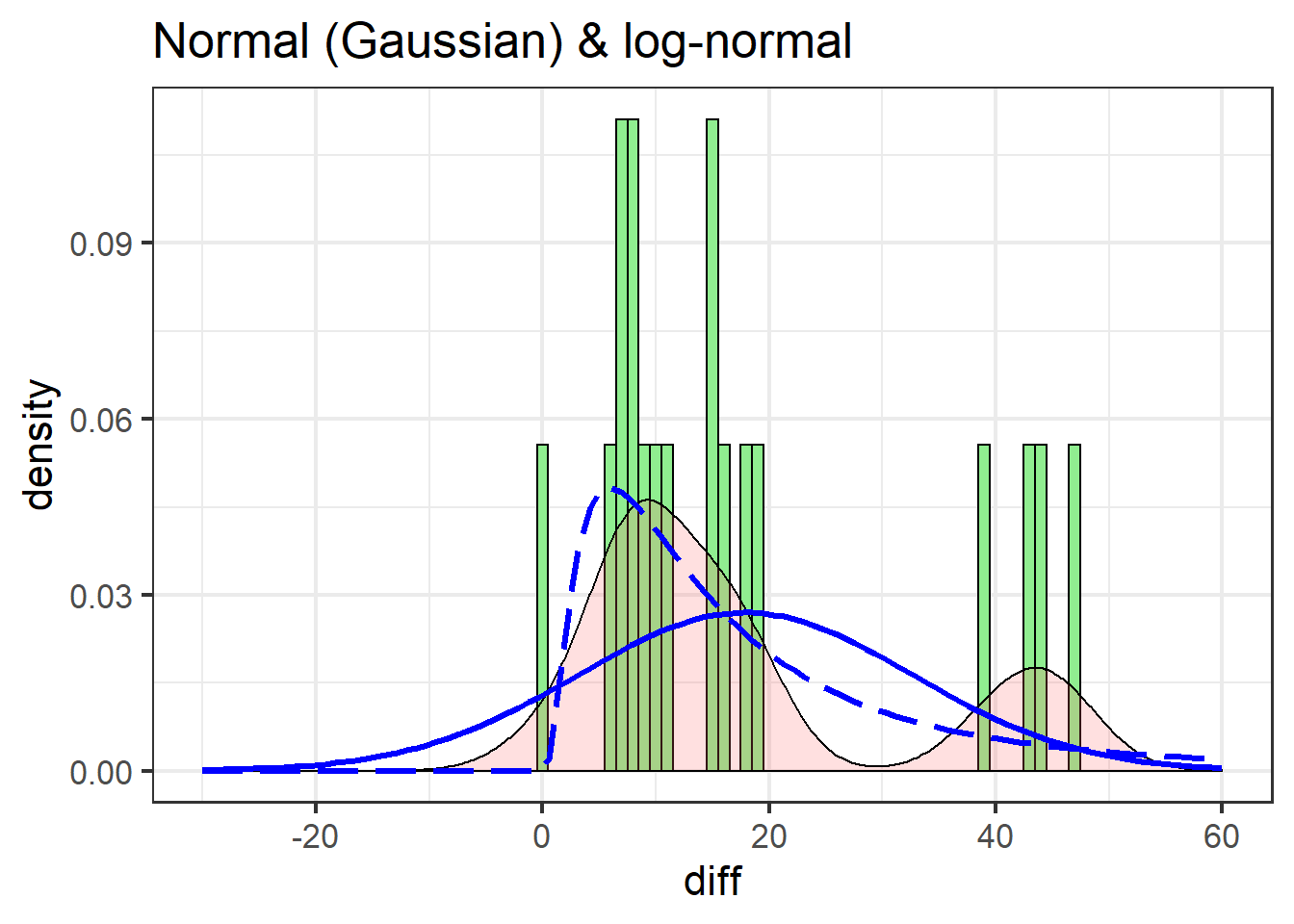

The normal distribution (solid line) is a poor fit for two main reasons:

It under-predicts every value
It over-predicts negative values, of which there are none in the actual data

The log-normal does better: it doesn’t predict any negative values and is decent at catching the peak between 0 and 10.

We can also explore a gamma distribution. Just putting in these data as they are will cause fitdistr to return an error, as the support for the gamma distribution – the range of potential values – is positive non-zero (\(x > 0\)); \(x \le 0\) is not allowed. These data include zero, but we can circumvent the limitation by adding a trivial positive non-zero value, 0.001:⁷

MASS::fitdistr(swha.dat$diff+0.001, "Gamma")

##      shape         rate   
##   0.81921940   0.04579237 
##  (0.23607979) (0.01778030)

The parameters for the gamma distribution, shape and rate, are calculated from the mean and standard deviation. The parameter list is passed to dgamma via args=:

swha_gg + stat_function(data=swha.dat, 
                        fun = dgamma, 
                        args=list(shape=1.86, 
                                  rate=0.101),
                        colour="darkred", 
                        size=1.1) + 
  stat_function(data=swha.dat, 
                fun = dlnorm, 
                args=list(meanlog=mean(log(swha.dat$diff+1)),
                          sdlog=sd(log(swha.dat$diff+1))),
                colour="blue", 
                lty=5,
                size=1.1)  +  
  xlim(c(-1, 60)) +
  labs(title = "Gamma + log-normal distribution")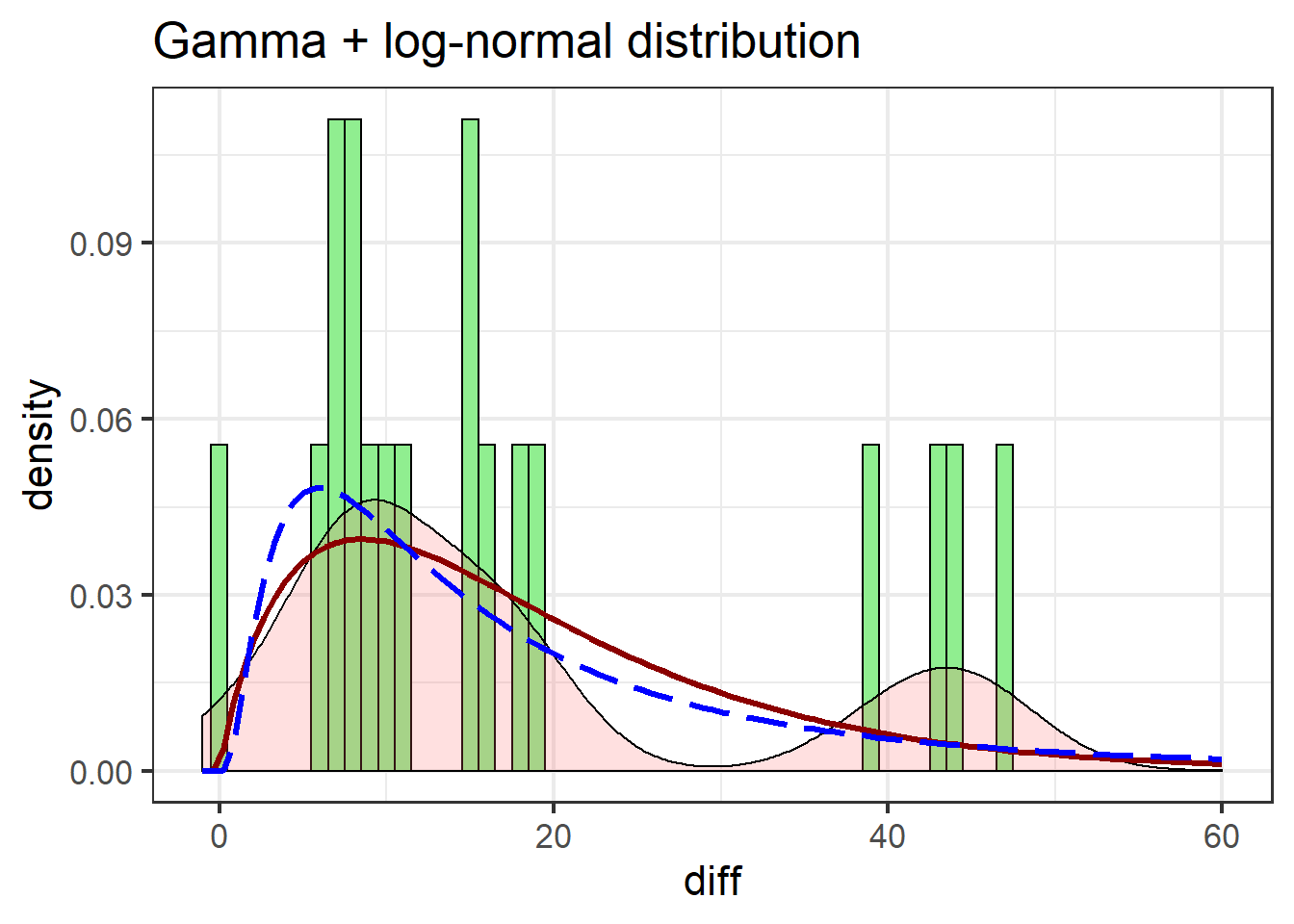

The gamma distribution isn’t terribly different from the log-normal, but notable improvements include the gamma more closely matching the first peak in the density estimate, and better estimating post-peak values.

Using `r*dist` functions

Having robust parameter estimates for data distribution is a powerful tool. For instance, once we know what the data ought to look like, we can generate many more observations than what we were limited to collecting from the field. These simulated data can be used in statistical models.

Confidence intervals are a basic statistical model we can apply to simulated data. Consider that the SWHA data are differences between before-fire and during-fire counts:

If there is an effect, it means the the difference is significantly different from zero.
Thus, at \(P = 0.05\), 95% of the time, the data should not include zero

This defines the 95% confidence interval – the range between which a random datapoint will occur at least 95% of the time.

We can simulate n number of observations from a specific distribution using r*dist functions:

swha_dist <- tibble(normal = 
                      rnorm(
                        n=1000, 
                        mean=mean(swha.dat$diff),
                        sd=sd(swha.dat$diff)), 
                      LogNormal = 
                       rlnorm(
                         n = 1000,                                                                       meanlog=mean(log(swha.dat$diff+1)),                                             sdlog=sd(log(swha.dat$diff+1))), 
                      gamma = 
                        rgamma(
                          n=1000, 
                          shape=1.86, 
                          rate=0.101 ) ) %>%
              gather(dist, value)
swha_dist

## # A tibble: 3,000 x 2
##    dist    value
##    <chr>   <dbl>
##  1 normal 20.6  
##  2 normal  7.92 
##  3 normal 30.8  
##  4 normal 16.6  
##  5 normal 24.1  
##  6 normal -0.810
##  7 normal -5.87 
##  8 normal 11.2  
##  9 normal 30.5  
## 10 normal 32.8  
## # … with 2,990 more rows

The simulated data can be interpreted as if we were able to go count Swainson’s Hawks 1000 times under three different scenarios: Their responses to fire followed a normal, log-normal, or gamma distribution.

From these data we calculate 95% confidence intervals to determine where observations are most likely to occur under each scenario. Confidence intervals are found via the quantile() function, which finds the value in a vector at each position identified in the prob= argument. In this case, we want to essentially trim the lowest 2.5% and 97.5% of the data, to focus on the center 95%:

 swha_dist %>%
  group_by(dist) %>%
    summarize(`2.5%` = round(quantile(value, prob=0.025,na.rm=TRUE), 0), 
              `97.5%` = round(quantile(value, prob=0.975,na.rm=TRUE), 0))

## # A tibble: 3 x 3
##   dist      `2.5%` `97.5%`
##   <chr>      <dbl>   <dbl>
## 1 gamma          2      54
## 2 LogNormal      2      79
## 3 normal       -11      47

Recall that a confidence interval that includes zero indicates that the data are not significantly different from zero, which in this case means there is no effect of fire attracting Swainson’s Hawks.

We can visualize the distributions of simulated data with respect to zero:

swha_dist %>%
  ggplot() + theme_bw(16) + 
    geom_hline(yintercept = 0, size=1.5, lty=2) + 
    geom_violin(aes(x=dist, y=value, 
                     fill=dist), 
                alpha=0.75, 
                show.legend = F) +
    coord_flip() + 
  geom_violin(data=swha.dat, 
              aes(x=1.5, y=diff), 
              fill=NA, size=1.5) + 
   geom_jitter(data=swha.dat, 
               aes(x=1.5, y=diff), 
               width = 0.1, 
               size=4, pch=21, stroke=1.5, 
               col="grey80", bg="grey20") +
   annotate("text", x=1.5, y=100, 
            label="Actual data", 
            size=6, fontface="bold")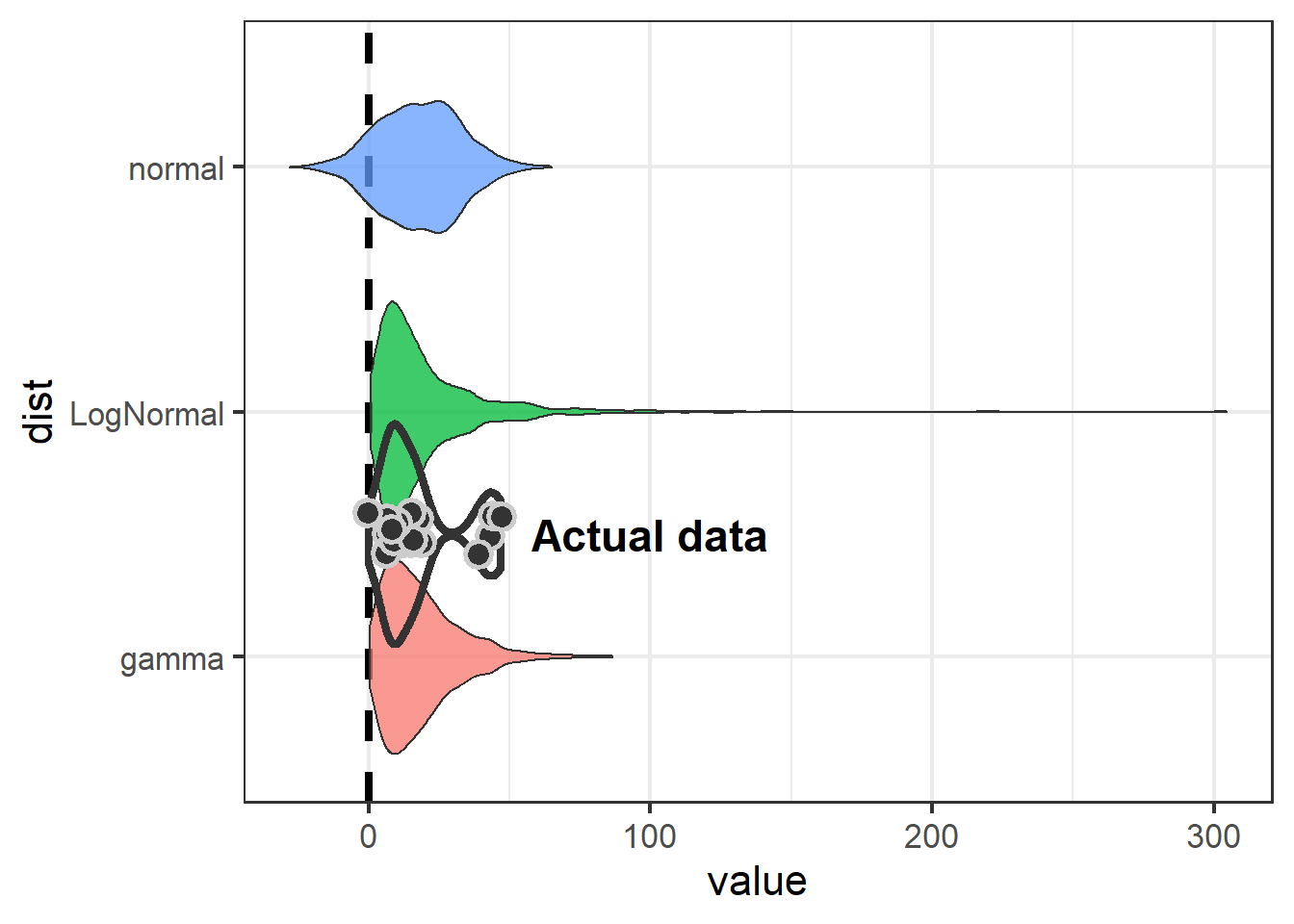

The take-away is that if we model Swainson’s Hawk response with a normal distribution, we aren’t going to detect an effect.

Because the normal distribution is symetrical and the mean of our data is close to zero, the normal distribution is going to include some negative numbers even though we never saw a negative number in our dataset. Both the log-normal and gamma distributions show an effect (neither 95% CI includes zero), but the gamma is preferable because it is less likely to over-estimate at the high end (51 vs 88).

The upshot of this example is that by using an alternative distribution, an effect was demonstrated for at least one species and the paper got published. But I have mixed feelings about whether this was the right approach.

Note that is a fairly colloquial use of the term “probability” and doesn’t actually reflect the logical construction of the statistical test we’d likely apply here.↩
MASS is one of those packages with functions that create conflicts with tidyverse functions, so I recommend not loading it to the session and using necessary functions from it directly with MASS::.↩
For other, not-normal distributions, parameters are calculated from the moments. fitdistr returns the parameters for those distributions, not \(\mu\) or \(\sigma^2\).↩
A Probability Density Function under which the entire area integrates to 1.0.↩
A third option, using a non-parametric test that doesn’t have assumptions about the distribution, will not be covered here because I neither use nor teach non-parametric tests ¯\_(ツ)_/¯ ↩
The gamma distribution has limitations, such as the requirement that all data be positive, non-zero. This is a feature, not a bug!↩
Sliding all observations like this is a translation as opposed to a transformation. ↩

Lesson 7 | Data distributions